Shafi Goldwasser and Zero Knowledge

by Paul Curzon, Queen Mary University of London

Shafi Goldwasser is one of the greatest living computer scientists, having won the Turing Award in 2012 (equivalent to a Nobel Prize). Her work helped turn cryptography from a dark art into a science. If you've ever used a credit card through a web browser, for example, her work was helping you stay secure. Her greatest achievement, with Silvio Micali and Charles Rackoff, is the "Zero knowledge proof".

Zero knowledge proofs deal with the problem that, to be really secure, security protocols often need to prove that some statement is true without giving anything else away (see "You are what you know"). A specific case is where an agent (software or human) wants to prove they know some secret, without actually giving the secret up.

Satisfy me this

There are three properties a zero knowledge proof must satisfy. Suppose Peggy is trying to convince Victor that some statement about a secret is true. Firstly, if Peggy's statement is true then Victor must be convinced of this at the end. Secondly, if it is not actually true, there must only be a tiny chance that Peggy can convince Victor that it is true. Finally, Victor must not be able to cheat in any way that means he learns more about the secret beyond the truth of the statement. Shafi and colleagues not only came up with the idea, but showed that such proofs, unlikely as they seem, were possible.

Biosecurity break-in

Imagine the following situation (based on a scenario by Jean-Jacques Quisquater). A top secret biosecurity laboratory is protected so only authorised people can get in and out. The lab is at the end of a corridor that splits. Each branch goes to a door at the opposite end of the lab. These two doors are the only ways in or out. The rest of the room is totally sealed (see diagram).

Now, Peggy claims she knows how to get in, and has told Victor she can steal a sample of the secret biotoxin held there if he pays her a million dollars. Victor wants to be sure she can get in, before paying. She wants to prove her claim is true, but without giving anything more away, and certainly not by showing him how she does it, or giving him the toxin. She doesn't even want him to have any hard evidence he could use to convince others that she can get in, as then he could use it against her. How does she do it?

"I can get in"

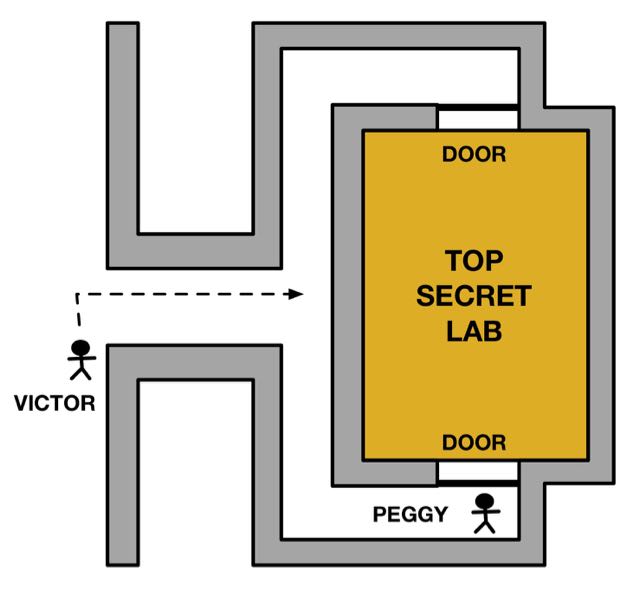
She needs a Zero knowledge proof of her claim "I can get in"! Here is one way. Victor waits in the foyer, unable to see the corridor. Peggy goes to the fork, and chooses a branch to go down then waits at the door. Victor then goes to the fork, unable to see where she is but able to see both exit routes. He then chooses an exit corridor at random and tells Peggy to appear there. Peggy does, passing through the lab if need be.

If they do this enough times, with Victor choosing at random which side she should appear, then he can be strongly certain that she really does know how to get in. After all, that is the only way to appear at the other side. More to the point, he still cannot get in himself and even if he records everything he sees, he would have no way to convince anyone else that Peggy can get in. Even if he videod everything he saw, that would not be convincing proof. A video showing Peggy appearing from the correct corridor would be easy to fake. Peggy has shown she can get into the room, but without giving up the secret of how, or giving Victor a way to prove she can do it to anyone else.

So, strange as it seems, it is possible to prove you know a secret without giving anything more away about the secret. Thanks to Shafi and her co-researchers the idea is now a core part of computer security.